Euclid's 47th problem, otherwise known as Pythagoras's theorem, is an important part of Masonic teachings. It's a bit unclear whether the usual B squared + C squared = A squared answer is all there is to it. It is usually depicted as a 3-4-5 triangle, or something similar. I found this one on the web, in an old Masonic manual. This link takes you to the source.
The Mason's traditionally trace their origins back as far as ancient Egypt, and the story of Hyram Abif. This construction links them to Giza, specifically G2.
[www.google.com]
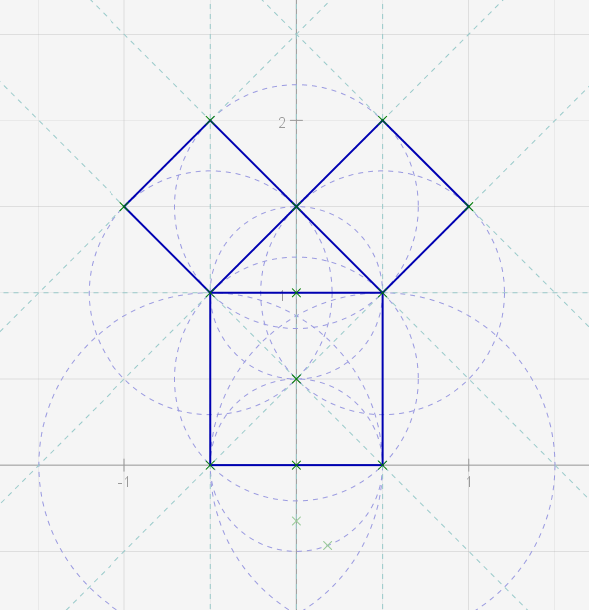
This is the 47th problem as depicted in the link. Not a 3-4-5 triangle, but a 2-sqrt2-sqrt2.
Image may be NSFW.
Clik here to view.
This is the rather archaic language that goes with it, showing the age of the publication.
Image may be NSFW.
Clik here to view.
This is a construction for the above figure, using compass and straight edge. As usual, it is based on the Vesica Piscis and then develops from there.
Image may be NSFW.
Clik here to view.
This is the image from the manual as constructed above.
Image may be NSFW.
Clik here to view.
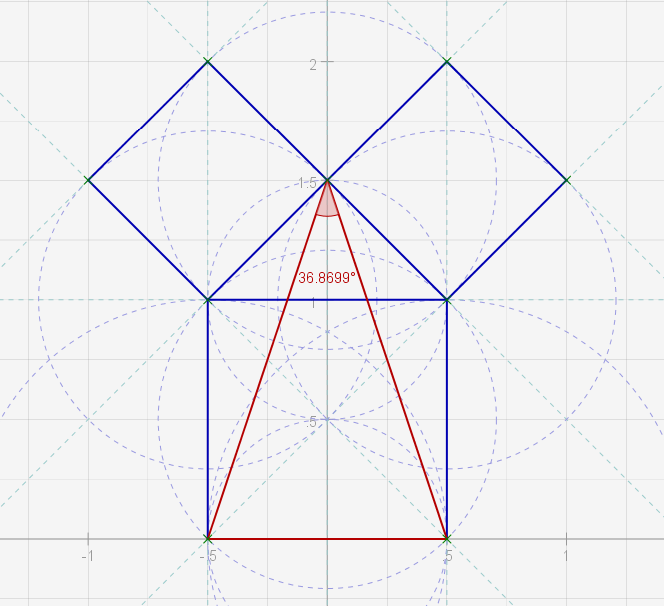
When the inner triangle is added its apex angle gives the first link to G2.
Image may be NSFW.
Clik here to view.
More of the angles naturally produced.
Image may be NSFW.
Clik here to view.
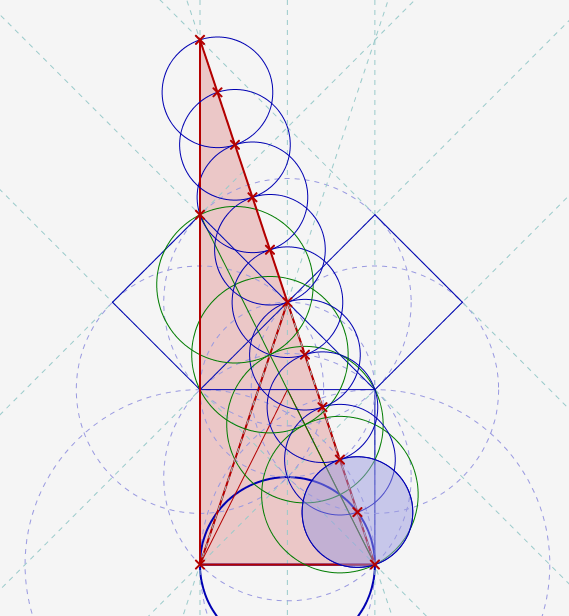
The "inner inner" triangle formed inside the larger square is the same one that was investigated in an earlier exercise. Its apex angle of 53.13 degrees being the same as G2's slope angles. The other angles here go together in very interesting ways,eg; 90 - 26.57 = 63.43; 26.57 x 2 = 53.14; 36.87 + 26.57 = 63.44; 36.87 x 2 = 73.74( G2 apex angle)
Image may be NSFW.
Clik here to view.
Extend the "inner inner" triangle legs and they are found to coincide with the original small square's corners, forming a larger version of the inner inner triangle( or half of it anyway)
Image may be NSFW.
Clik here to view.
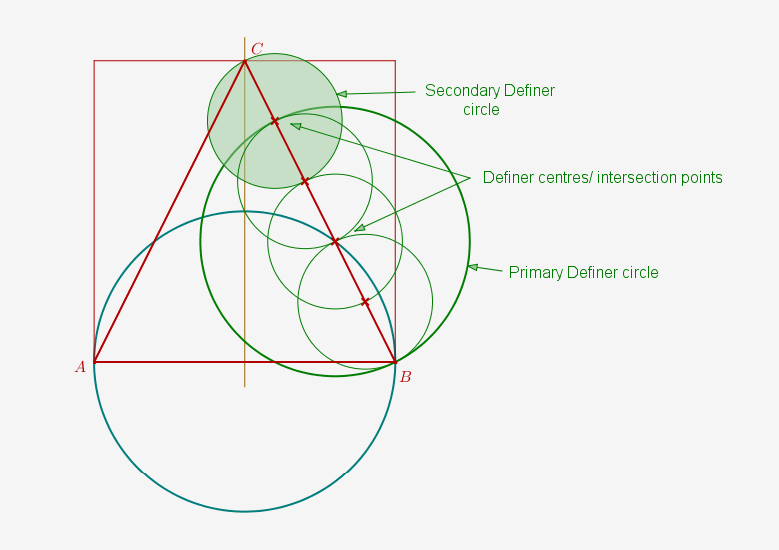
This is how the "inner inner" triangle was originally analysed using the Definer circle method.
[grahamhancock.com]
This particular triangle was found to correspond to a secondary Definer. The primary Definer being too large to fit.
Image may be NSFW.
Clik here to view.
The secondary Definers added, with the difference between the primary and secondary shown.
Image may be NSFW.
Clik here to view.
This new construction reveals a different way of applying the Definer circle method of analysis. Normally it revolves around the relationship between an Isosceles triangle's baseline circle and it's altitude foot to baseline corner circle. This time, with the "inner inner" triangle extending as it has, the baseline circle has effectively been halved in size, resulting in smaller Definers.
This is what happens when a primary Definer from the "inner inner" triangle is applied to the extended triangle leg, in heavy green here. It is seen to fit perfectly. In effect, the primary Definers become secondary Definers for the extended leg
Image may be NSFW.
Clik here to view.![]()
This is how it works out when the original inner triangle has its Definers added
Image may be NSFW.
Clik here to view.![]()
When the original inner triangle is extended in the same way it effectively doubles in length so consequently matches the primary Definers perfectly. As before, this development goes on forever.
Image may be NSFW.
Clik here to view.![]()
The Mason's traditionally trace their origins back as far as ancient Egypt, and the story of Hyram Abif. This construction links them to Giza, specifically G2.
[www.google.com]
This is the 47th problem as depicted in the link. Not a 3-4-5 triangle, but a 2-sqrt2-sqrt2.
Image may be NSFW.
Clik here to view.
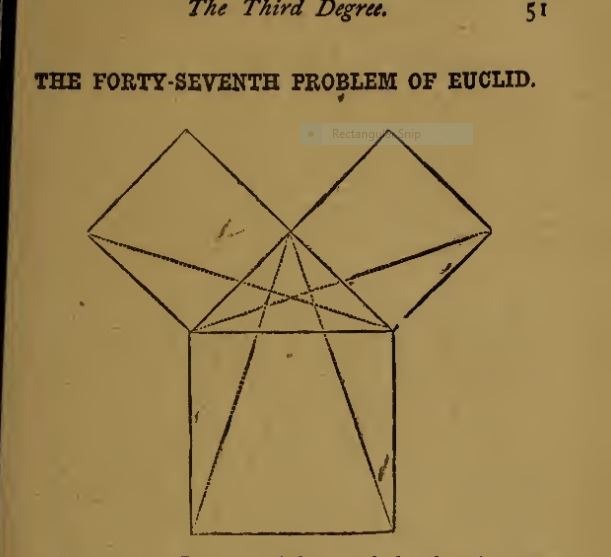
This is the rather archaic language that goes with it, showing the age of the publication.
Image may be NSFW.
Clik here to view.

This is a construction for the above figure, using compass and straight edge. As usual, it is based on the Vesica Piscis and then develops from there.
Image may be NSFW.
Clik here to view.

This is the image from the manual as constructed above.
Image may be NSFW.
Clik here to view.
When the inner triangle is added its apex angle gives the first link to G2.
Image may be NSFW.
Clik here to view.
More of the angles naturally produced.
Image may be NSFW.
Clik here to view.
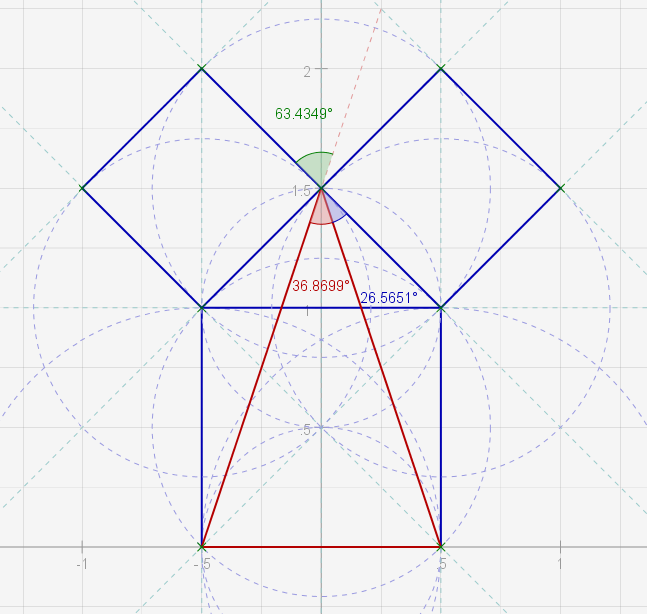
The "inner inner" triangle formed inside the larger square is the same one that was investigated in an earlier exercise. Its apex angle of 53.13 degrees being the same as G2's slope angles. The other angles here go together in very interesting ways,eg; 90 - 26.57 = 63.43; 26.57 x 2 = 53.14; 36.87 + 26.57 = 63.44; 36.87 x 2 = 73.74( G2 apex angle)
Image may be NSFW.
Clik here to view.
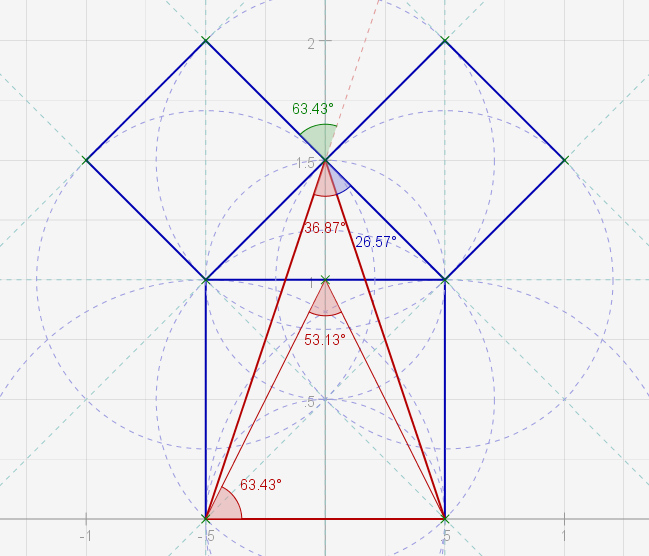
Extend the "inner inner" triangle legs and they are found to coincide with the original small square's corners, forming a larger version of the inner inner triangle( or half of it anyway)
Image may be NSFW.
Clik here to view.
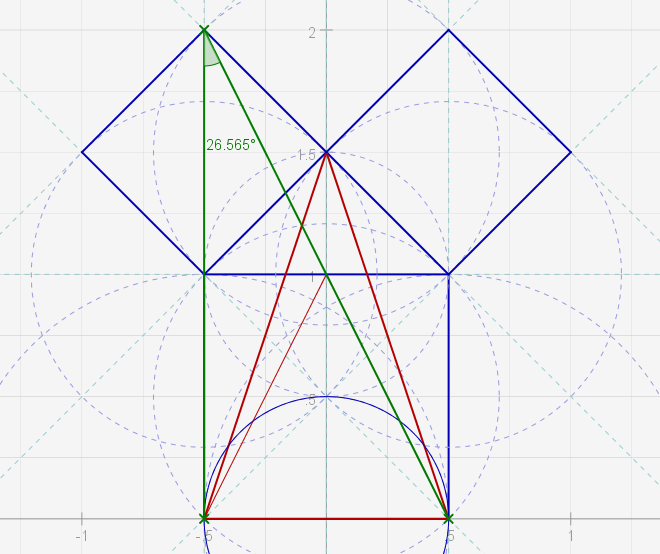
This is how the "inner inner" triangle was originally analysed using the Definer circle method.
[grahamhancock.com]
This particular triangle was found to correspond to a secondary Definer. The primary Definer being too large to fit.
Image may be NSFW.
Clik here to view.
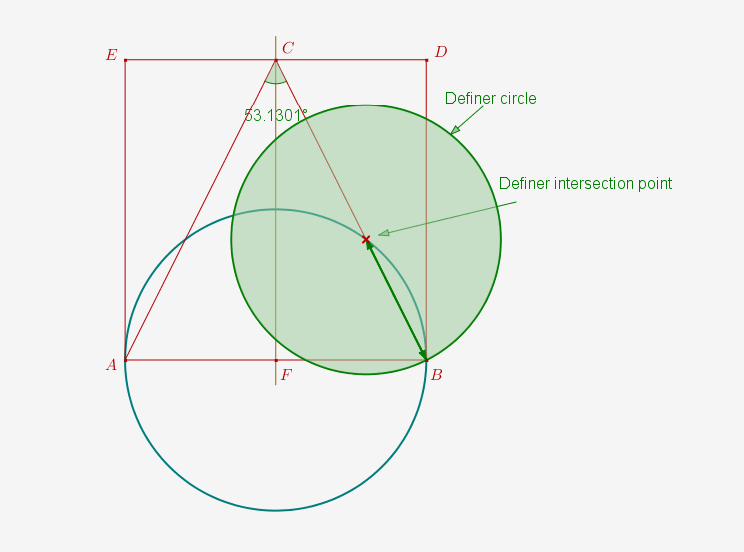
The secondary Definers added, with the difference between the primary and secondary shown.
Image may be NSFW.
Clik here to view.
This new construction reveals a different way of applying the Definer circle method of analysis. Normally it revolves around the relationship between an Isosceles triangle's baseline circle and it's altitude foot to baseline corner circle. This time, with the "inner inner" triangle extending as it has, the baseline circle has effectively been halved in size, resulting in smaller Definers.
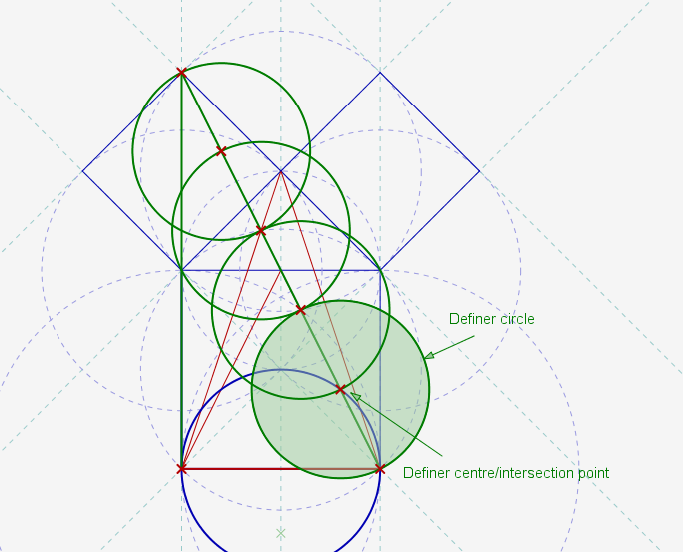
This is what happens when a primary Definer from the "inner inner" triangle is applied to the extended triangle leg, in heavy green here. It is seen to fit perfectly. In effect, the primary Definers become secondary Definers for the extended leg
Image may be NSFW.
Clik here to view.
This is how it works out when the original inner triangle has its Definers added
Image may be NSFW.
Clik here to view.
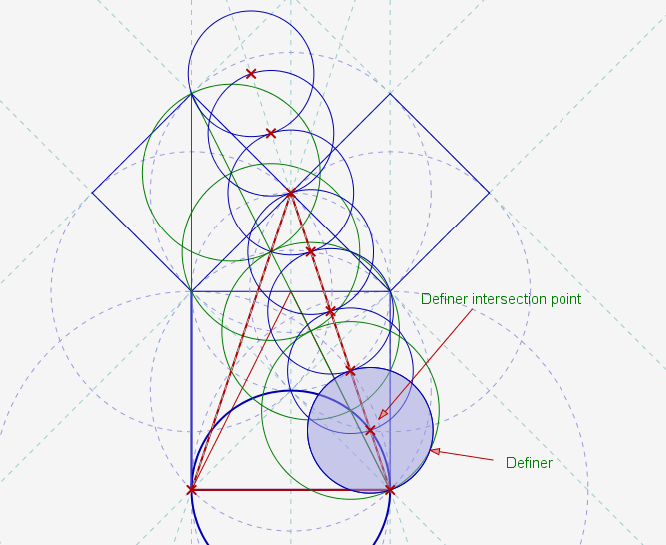
When the original inner triangle is extended in the same way it effectively doubles in length so consequently matches the primary Definers perfectly. As before, this development goes on forever.
Image may be NSFW.
Clik here to view.